A Closer Look at the Impacts of Olympic Averaging of Prices and Yields
Several provisions of the 2014 Farm Bill depend critically on revenue thresholds calculated from the product of the Olympic average of 5-year trailing national marketing year average prices, and the Olympic average of trailing county yields. This post more closely examines the implications of using truncated samples or Olympic averages to construct measures termed Benchmark Revenue, and also examines some specific implications given the price and yield patterns that occurred recently, and thus which are included in near-term future Benchmark Revenue calculations.
The term, “Olympic Average” stems from the practice used in determining average scores across Olympic judges who might have positive or negative biases about the performer, independent of the performance. The truncation of the scores is intended in essence to limit the impacts of outliers, or data that are not representative of the informational content of the process generating the observation. A judge could not thereby unduly influence the outcome of athletes from his/her home country by providing unrealistically high scores, nor disadvantage a competitor from a disfavored country. Importantly, the process is designed for cases where the extreme observations are thought to not be generated by the same process as the others, not for cases when there are simply random but informative observations. More formally, the process of using truncated samples can reduce bias in estimates of central tendency, but often results in less accuracy, or more variation between actual and calculated values.
The process becomes much more complex when two related series such as prices and yields are involved, as the product of the average of each series is not generally equal to the average of the series of products. Because price and yield shocks are generally negatively correlated, the impact of using truncated averages prior to multiplying can create substantial differences from the average revenue that would have resulted from first multiplying the two series and then averaging. The process stipulated in the Farm Bill thus creates a Benchmark Revenue measure that may differ systematically from the concept of the average of actual revenue against which the payments are calculated.
Importantly, this post explores implications of the process selected by Congress for construction of the Benchmark Revenue. It is neither intended to support nor criticize a particular process, only to better illuminate the implications related to selection of options, and how the differences depend on the strength of correlation between prices and yields; a feature in itself that differs across major commercial production regions. Finally, the Farm Bill is being implemented at a point in time with known information about the pattern of recent prices and yields such that there are strong indications for the next several calculations of Olympic average prices due to the rolling window and date of the lowest price in the most recent five-year period, and the replacement of prices below the reference price. These facts also impact the relative desirability of the alternatives offered.
The materials presented first use a stylized explanation of the reason that taking averages of related price and yield series and then multiplying results in a different value than averaging revenue directly. This fact holds whether an Olympic average is used or not. The impact of truncating part of the sample has increasingly important implications in regions where the price and yield are strongly negatively related, and less impact where there is less dependence. Actual county-level yield data from the states in the Group 1 crop insurance region (IL, IN, IA, NE, MN) are used to identify the magnitude of differences due to the averaging process employed, which in turn creates implications for program selection.
A small amount of technical detail may help, but may also be skipped without loss of continuity. The expression for the expected value (or average) of the product of two random variables such as price (P) and yield (Y) which together determine expected revenue, or E(P*Y) is:
- E(P*Y) = E(P)*E(Y)+Cov(P,Y)
Where E(.) refers to the expected value, and Cov(.) refers to the covariance between the items identified. If P and Y are uncorrelated, then Cov = 0 and the average revenue is the same as the product of the average of price and yield. However, it is generally understood that prices and yields are negatively related in major production regions — another way of saying that the covariance is negative. Thus, averaging P and Y first and then multiplying will directionally overstate the actual average revenue generated in that location. The degree to which these differ depends directly on the strength of the correlation. There is nothing wrong in principle with a benchmark that is greater than the average of the actual, it is simply important to understand the implication of the calculation and its impact on associated payments.
To better understand why products of averages result in different values than averages of the products, consider two series referred to below as P and Y which might be thought of as differences from their typical values. Each can only take on the values of 1,2,3,4,or 5 with equal likelihood, and thus the average of each is 3, and the product of each of the averages is 9 under either a simple average or under an Olympic truncation eliminating the high and the low of each. Table 1 shows two of the possible patterns with the values in the left side displaying perfect negative correlation and the pattern on the right side showing positive correlation. The top half of Table 1 shows a complete sample and the bottom half shows the outcomes after applying the Olympic average truncation.
Importantly, the samples of the numbers from 1-5 are the same in every case, so the average and the Olympic average of each series is 3. If you multiply the average P by the average Y, you always get 9. However, the top left section shows the case most similar to that which an actual producer would experience with negative price and yield correlation. The “true” long run average is 7 in this case, but use of an Olympic average to set the benchmark would result in a value of 8.33, and use of Olympic averages of P and Y prior to averaging would again result in a value of 9. The higher benchmark than true average has implications for the frequency that the actual revenue calculation would fall below the benchmark. In the typical case, the more negatively correlated the series, the greater the advantage to the producer of the use of the average price times yield to construct the benchmark.

The degree to which the Olympic averages multiplied together depart from the “true” is also slightly dependent on sample length as random departures from the true can persist in the sampled data period longer with longer sample periods. In the case of actual commodity markets, there is likely some persistence in in prices through carryover stock effects, as from 2012 to 2013, but no memory within the yield series as there is little evidence that yields are related year to year. However, even if a series is perfectly random, the moving Olympic average of the historicals creates persistence, and thus can result in periods effectively “stuck” above or below the true average. To illustrate this effect, a simple model was developed to sample from yields with an average of exactly 175 and a standard deviation of 29 to somewhat mimic central Illinois conditions. Importantly, in Figure 1 below, there is absolutely no memory in the base process generating yields so there is exactly the same likelihood for each subsequent observation to be either above or below the average of 175 regardless of whether its prior value was above or below 175. Despite the randomly constructed series, the Olympic average of preceding yields stays above or below the line with persistence due to the simple fact that extreme highs and lows tend to be removed from the retained sample for several years in a row as the sample window rolls forward. For context, a 7 year Olympic average is also displayed to illustrate the additional lagging effect induced with longer sample averaging periods. The relationship helps to explain why average revenue programs seem more attractive when implemented in periods that involve generally falling prices relative to their recent prior values.
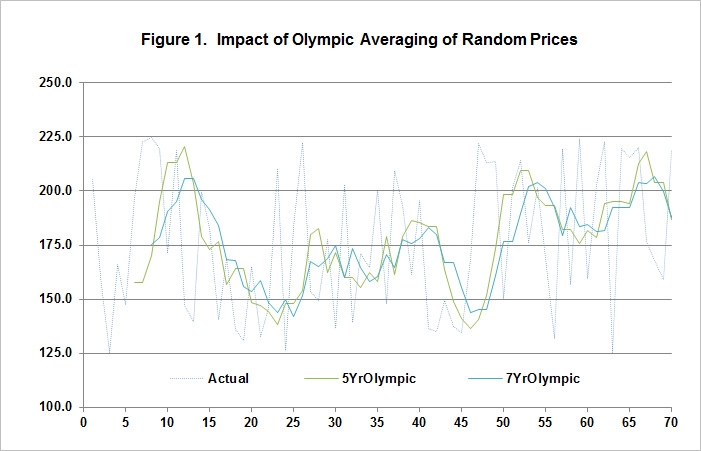
The preceding materials are intended to help appreciate some implications of the process used in the development of benchmark revenue measures as used in the Farm Bill ARC County program in particular, but it is important to also assess whether there important empirical effects in use, or if only an academic exercise. To address this issue, county yield data were collected from NASS for counties in the Group 1 states, where much of the corn and soybean production occurs (IL, IN, IA, MN, NE), along with marketing year average prices, all from 1975 to present (though a few of the 2013 yield data are still incomplete). The $3.70 substitution price was not implemented in the historic data and no yield substitutions were made, but the calculations were otherwise meant to mimic Farm Bill ARC-County provisions.
For each county, the simple correlation between MYA prices and county yields was first calculated in difference form. Table 2 shows the simple average correlation between price and yield changes across all counties (unweighted) by state over the period 1975 to 2013 (note: the values are virtually unchanged for the period from 1995 to 2013 as well). These values are substantially below zero indicating the potential for a meaningful difference to exist between the product of the Olympic average of prices and yields, and the actual average revenue.

Next, the actual revenue for each county was constructed (actual yield times MYA price) at each county along with the associated Olympic average price, Olympic average yield, and Olympic average of actual revenue. One question to ask is how close are the Benchmark Revenue measures to the average of the actual available revenue as defined in the Farm Bill. The results help confirm the point made earlier that the process of averaging P and Y separately will overstate the mean of the actual product under correlated outcomes, but that the Olympic averaging process does not exacerbate the difference. Across all counties from 1980 to 2013 (the first five years were used to initiate the Olympic averaging), the Benchmark Revenue is only $3.69 above the average of actual available revenue, and is as intended far less variable. However the time pattern reveals another important issue as the positive differences are greatest during time periods following higher than average prices. If the average of the differences is taken from 2009-2013, the difference increases to $7.90/acre. Furthermore, the greatest individual county differences match the areas with the most negative correlations to prices as expected.
A visual depiction of the relationships may help understand the cause. In the panels below, information related to prices, and to yields in Champaign County, Illinois is provided to better identify the causes of potential divergences. As can be seen in the first panel, the smoothing of prices, either by the use of an Olympic average, or had the simple 5-year average been used, creates a lagging effect as well. Because prices are above the longer term average, and due to the elimination of the lowest price from the oldest point in the five year sample, it is also clear that the Olympic average of the MYA prices will likely move to $5.29 or higher in 2014 (as the rolling off of 2009 means that any 2014 price below the 4th highest price of $4.46 will result in the same Olympic Average of the prior 5 years’ prices). In the second panel, the effect of smoothing yields through the Olympic averaging process is evident as the influence of 2012 for example in much of the cornbelt will be eliminated, but the impact of multiple years of relatively higher prices remains. As a result, the Farm Bill Benchmark Revenue will continue to climb and is more likely to be above actual revenue in the near term future due to the induced persistence of the moving averaging effect and the additional persistence of the Olympic averaging process. The final panel shows the difference between the calculated Benchmark Revenue and two revenue indexes of interest. The Benchmark less the Olympic average of actual revenue and the Benchmark less the simple average of actual revenue show similar patterns, except that the Olympic average of actual revenue is a bit smoother. The important feature is that the difference is greatest near the end of the sample period as a result of the pattern of prices experienced. This difference increases the attractiveness in the near term of the ARC program of course, as the likelihood for payments is increased as a result as well, especially if actual revenue falls below recent averages as is expected. It is also important to note that the opposite effect could occur in the future if prices were to increase for a substantial period and result in Benchmark Revenue values that understate actual expected revenue. Finally, the impact of the effect of the correlation appears modest compared to the impact of the averaging process itself during periods when prices are above or below longer term trends.


Note: The views expressed herein are solely the author’s opinions and do not necessarily reflect those of others or entities with whom professionally affiliated. All errors and omissions are the author’s alone.
Disclaimer: We request all readers, electronic media and others follow our citation guidelines when re-posting articles from farmdoc daily. Guidelines are available here. The farmdoc daily website falls under University of Illinois copyright and intellectual property rights. For a detailed statement, please see the University of Illinois Copyright Information and Policies here.







