Sensitivity Analysis of New Corn and Soybean Pricing Models
In the farmdoc daily article of April 6, 2016 we offered a new specification for the relationship between the marketing year ending stocks-to-use ratio and the marketing year average farm price for corn and soybeans. We used the models in a farmdoc daily article of April 13, 2016 to make price forecasts for the 2016-17 marketing year based on alternative corn and soybean balance sheet projections. We also used the models in a farmdoc daily article of April 22, 2016 to make projections of “new era” average prices and found that these were very consistent with earlier projections based on a simpler methodology. Because the new stocks and price models are based on a stronger economic foundation, we were more confident in these results. One issue we have not investigated is the sensitivity of the new models and forecasting results to alternative functional forms. Since the relationship between price and the stocks-to-use ratio is presumed to be inherently non-linear, it is important to determine the degree of sensitivity to alternative ways of modeling this non-linearity. In this article, we first review our benchmark reciprocal regression models for corn and soybeans and then estimate linear-logarithmic and logarithmic-logarithmic (“double-log”) specifications for comparison. Finally, we compare 2016-17 price forecasts and new era average price projections for the three alternative specifications to quantify the degree of sensitivity.
Review of New Ending Stocks and Price Models
The marketing year ending-stocks-to use ratio is a widely used indicator of the supply and demand “tightness” of corn and soybean market conditions and is very commonly used to project prices. Tomek and Kaiser (2014, p. 378) classify price and ending stocks-to-use regression models as “price determination equations” rather than formal structural models of supply and demand. They point out the complexity of realistic structural models that have separate equations for supply and the various demand categories. As a result, analysts often turn to, “…graphs, tables, and simple regression models of price determination to summarize information.” They also helpfully observe that, “The research objective may be to provide a forecasting tool, but more generally, the analysis helps the researcher depict current economic conditions relative to the historical evidence.” The bottom-line is that these types of models, while useful in forecasting, cannot be directly derived (at least easily) from underlying structural and mathematical models of supply and demand.
In a recent article (farmdoc daily, April 6, 2016), we estimated a base reciprocal regression model of the U.S farm price of corn and soybeans and the ending stocks-to-use ratio for the period 1990-91 through 2005-2006, skipped 2006-07 as a transition year, and then estimated relationships after 2005-06 that are exactly parallel to the base period model. We selected the reciprocal functional form because it is simple and imposes the presumed non-linear relationship between price and the stocks-to-use ratio. As Tomek and Kaiser (2014, p. 379) note, “This accommodates the idea that, as current stocks approach zero (but cannot be less than zero), price must necessarily rise sharply to ration these stocks among competing demands.” In our new model, we assumed the slope is unchanged between the base period and relationships after 2005-06, but the intercept varies in the latter period to reflect demand shifts that occurred after 2005-06. We further grouped the years after 2005-06 into four demand scenarios for corn (weak, moderate 1, moderate 2, and strong) and three demand scenarios for soybeans (weak, moderate, and strong).
The estimated pricing model of the relationship between the average marketing year price of corn and the ending stock-to-use ratio over 1990-91 through 2015-16 is presented in Figure 1. We used a reciprocal regression specification as follows:
- Corn Price = a + b (1/Corn Stocks-to-Use Ratio) + c DW + d DM1 +e DM2 + f DS,
where DW is a dummy variable that takes on a value of 1 during weak demand years after 2005-06 and 0 otherwise, DM1 is a dummy variable that takes on a value of 1 during moderate demand 1 years after 2005-06 and 0 otherwise, DM2 is a dummy variable that takes on a value of 1 during moderate demand 2 years after 2005-06 and 0 otherwise, and DS is a dummy variable that takes on a value of 1 during strong demand years after 2005-06 and 0 otherwise. The intercept coefficient, a, in this reciprocal specification has the interesting interpretation as the estimated minimum price for the period under consideration. The coefficients on the dummy variables (c, d, e, and f) simply shift this estimated minimum price up or down by the magnitude of the dummy coefficient (in $ per bushel). The “slope” coefficient, b, does not have the usual interpretation of the change in price for a one-unit increase in the stocks-to-use ratio because of the reciprocal specification. Instead, at any given stocks-to-use ratio, the change in price for a one-unit increase in the stocks-to-use ratio is -b/(stocks-to-use ratio)2. The complete estimation results for the reciprocal model specification for corn can be found in Appendix Table 1. The reader is referred to our earlier article (farmdoc daily, April 6, 2016) for a more detailed discussion of the new model.

The estimated pricing model of the relationship between the average marketing year price of soybean and the ending stock-to-use ratio over 1990-91 through 2015-16 is presented in Figure 2. We again used a reciprocal regression specification:
- Soybean Price = a + b (1/Soybean Stocks-to-Use Ratio) + c DA + d DW + e DM + f DS
where DA is a dummy variable that takes on a value of 1 during the Asian financial crisis years of 1999-00 through 2001-02 and 0 otherwise, DW is a dummy variable that takes on a value of 1 during weak demand years after 2005-06 and 0 otherwise, DM is a dummy variable that takes on a value of 1 during moderate demand years after 2005-06 and 0 otherwise, and DS is a dummy variable that takes on a value of 1 during strong demand years after 2005-06 and 0 otherwise. The complete estimation results for the soybean reciprocal model specification can be found in Appendix Table 2. The interpretation of the estimated model coefficients is the same as discussed above for corn.

Sensitivity Analysis
Tomek and Kaiser (2014, p. 379) note that a variety of non-linear functional forms can be used in ending stocks models. We consider two in order to assess the sensitivity of our modeling results to this choice: the linear-logarithmic (lin-log) specification and the logarithmic-logarithmic (log-log) specification. The lin-log models for corn and soybeans are shown below:
- Corn Price = a + b ln(Corn Stocks-to-Use Ratio) + c DW + d DM1 +e DM2 + f DS, and,
- Soybean Price = a + b ln(Soybean Stocks-to-Use Ratio) + c DA + d DW + e DM + f DS.
Not that “ln” indicates the natural logarithm of the stocks-to-use ratio. In this case, the intercept coefficient, a, is interpreted as the expected price when the stocks-to-use ratio takes on a value of 1. The coefficients on the dummy variables (c, d, e, and f) simply shift this expected price up or down by the magnitude of the dummy coefficient (in $ per bushel). The “slope” coefficient, b, once again does not have the usual interpretation of the change in price for a one-unit increase in the stocks-to-use ratio because of the logarithmic transformation of the stocks-to-use ratio. Instead, at any given stocks-to-use ratio, the change in price (in $ per bushel) for a one-percentage point increase in the stocks-to-use ratio is b/(stocks-to-use ratio).
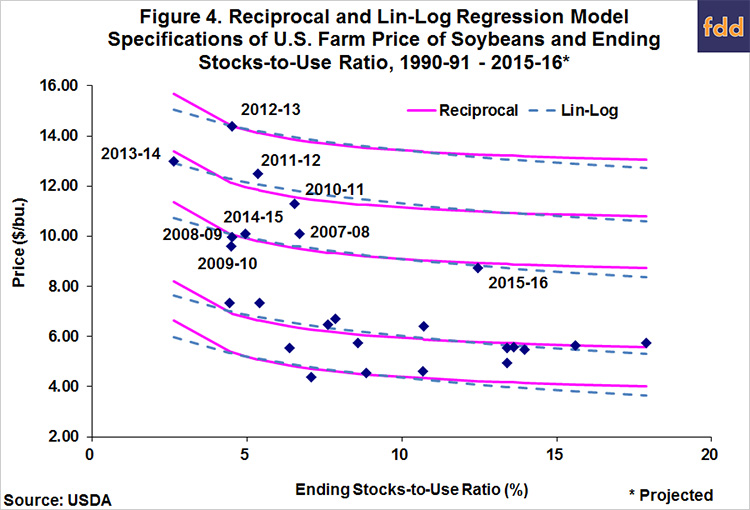
The estimated lin-log pricing models for corn and soybeans over 1990-91 through 2015-16 are presented in Figures 3 and 4, respectively, along with the reciprocal model regressions. Visual inspection of the charts reveals very little difference in the estimation results for the lin-log models in comparison to the reciprocal models. In fact, over a wide range of stocks-to-use ratios there is virtually no difference. Differences only emerge at extremely small or large stocks-to-use ratios, and even these differences are relatively small. Complete estimation results for the lin-log model specification for corn and soybeans can be found in Appendix Tables 3 and 4, respectively.

The log-log models for corn and soybeans are shown below:
- ln(Corn Price) = a + b ln(Corn Stocks-to-Use Ratio) + c DW + d DM1 +e DM2 + f DS,
and,
- ln(Soybean Price) = a + b ln(Soybean Stocks-to-Use Ratio) + c DA + d DW + e DM + f DS.
The only change from the lin-log model is that the natural logarithm is applied to both price and the stocks-to-use ratio. This seemingly small change, however, has a significant change on the interpretation of the regression model coefficients. In this case, the intercept coefficient, a, is interpreted as the expected natural logarithm of price when the stocks-to-use ratio takes on a value of 1. Hence, the intercept has to be exponentiated in order to obtain the expected price when the stocks-to-use ratio is 1. The coefficients on the dummy variables (c, d, e, and f) shift the expected natural logarithm of price up or down by the magnitude of the dummy coefficient. This has the practical effect of imposing equal percentage shifts in the regression relationship rather than equal dollar shifts as with the reciprocal and lin-log specifications. The “slope” coefficient, b, in the log-log regression has a very useful elasticity interpretation. That is, at any given stocks-to-use ratio, the coefficient b estimates the percentage change in price for a one-percentage point increase in the stocks-to-use ratio.
The estimated log-log pricing models for corn and soybeans over 1990-91 through 2015-16 are presented in Figures 5 and 6, respectively, along with the reciprocal model regressions. Visual inspection of the charts reveals substantial differences in the estimation results for the log-log models in comparison to the reciprocal models (and implicitly the lin-log models). Especially large differences can be seen for small and large stocks-to-use ratios. For example, at a 15 percent stocks-to-use ratio and strong demand, the forecast corn price in Figure 5 is $6.01 for the reciprocal model and $5.26 for the log-log model, a difference of $0.75 per bushel. The driver of the difference in the results for the log-log model is the assumption that the differences between the regression relationships are in percentage terms rather than dollar terms. This can be seen most easily in Figures 7 and 8, which remove the reciprocal model regression lines. It can now be readily seen that the difference between the log-log regression lines becomes larger in dollar terms with smaller stocks-to-use ratios in order to keep the percentage price difference between the relationships constant. Complete estimation results for the log-log model specification for corn and soybeans can be found in Appendix Tables 5 and 6, respectively.




With the estimation results for the lin-log and log-log in hand, we can now more directly evaluate how much difference the selection of functional form makes on 2016-17 price forecasts. The stocks-to-use ratio must be projected first and then the appropriate scenario for demand has to be specified. We illustrated that two-step process for the 2016-17 marketing year using alternative balance sheet projections for corn and soybeans in a farmdoc daily article of April 13, 2016. Table 1 includes price forecasts for the stocks-to-use ratios for corn and soybeans projected under the “Irwin/Good” balance sheets for all three regression model specifications. The differences in the price forecasts turn out to be very small across the three models, largely due to the fact that the forecasts assume a weak demand scenario and the stocks-to-use ratios are near the median for each market. Somewhat larger differences could be generated, particularly for the log-log model, at small or large stocks-to-use ratios.

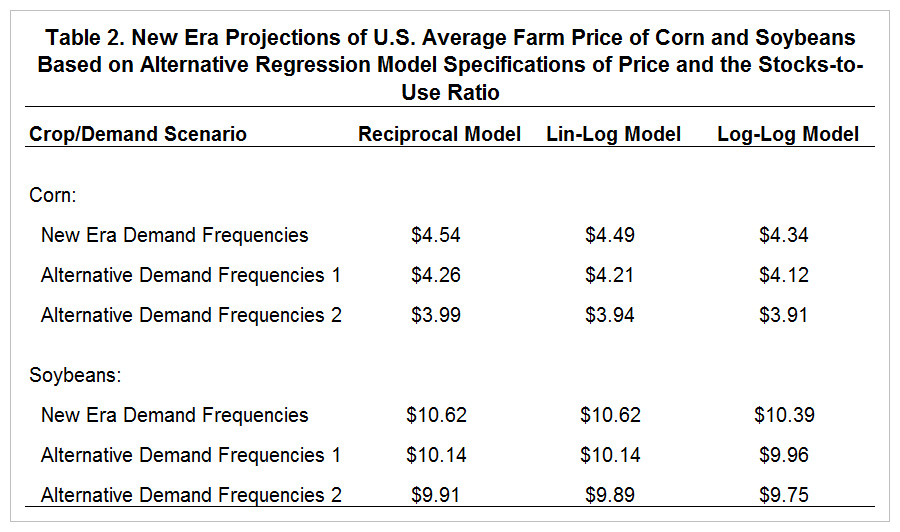
We next extend the analysis in our farmdoc daily article of April 22, 2016 of new era price projections for corn and soybeans using the lin-log and log-log regression models. Since the regression models project the farm price of corn and soybeans for a wide range of stocks-to-use ratios, we use the same method of converting the relationships to a single average price that we used in our previous article. Readers are encouraged to consult that article for details of the computations. Table 2 contains the long-term average price projections for corn and soybeans based on the ending-stocks-to use ratios for the past 26 years and the assumed frequency of weak, moderate, and strong demand scenarios. The new era scenario assumes the frequency of weak, moderate, and strong demand that occurred during the last nine marketing years. The two alternative scenarios assume higher frequencies of the weak demand conditions in order to provide more conservative average price projections. Once again, negligible differences are observed between the reciprocal and lin-log projections, at most $0.05. However, larger differences emerge between the log-log projections and the other two specifications. For example, with new era demand frequencies, the log-log regression model results in a long-term average price projection for corn of $4.34 compared to $4.54 based on the reciprocal model. This is a bit more than a 4 percent difference in the average price projections. This difference can be traced to the much steeper sloped regression relationships under the log-log specification.
Implications
We recently developed new specifications for the relationship between the marketing year ending stocks-to-use ratio and the marketing year average farm price for corn and soybeans and used these new models to forecast prices for the 2016-17 marketing year as well as generate long-term average price projections. The sensitivity of projections to modelling assumptions is always important to consider. Here, we investigated the sensitivity of the new models and forecasting results to alternative functional forms. We estimated linear-logarithmic and logarithmic-logarithmic (“double-log”) specifications for comparison to our base reciprocal model specification. We found only negligible differences in 2016-17 price forecasts across the specifications. Somewhat larger differences were found for long-term average price projections, particularly for the log-log specification. But, even then the largest differences amounted to only about 4 percent of the average price level. Overall, we conclude that our original reciprocal model regression results are relatively insensitive to the assumed functional form. While there is always uncertainty about the validity of model specifications, this reinforces our earlier conclusion that the new models provide useful benchmarks when forecasting corn and soybean prices.
References
Irwin, S., and D. Good. "The New Era of Corn and Soybean Prices Is Still Alive and Kicking."farmdoc daily (6):78, Department of Agricultural and Consumer Economics, University of Illinois at Urbana-Champaign, April 22, 2016.
Irwin, S., and D. Good. "Forming Corn and Soybean Price Expectations for 2016-17."farmdoc daily (6):71, Department of Agricultural and Consumer Economics, University of Illinois at Urbana-Champaign, April 13, 2016.
Irwin, S., and D. Good. "The Relationship between Stocks-to-Use and Corn and Soybean Prices: An Alternative View."farmdoc daily (6):66, Department of Agricultural and Consumer Economics, University of Illinois at Urbana-Champaign, April 6, 2016.
Tomek, W.G., and H.M. Kaiser. Agricultural Product Prices, Fifth Edition. Cornell University Press: Ithaca, NY, 2014.
Appendices






Disclaimer: We request all readers, electronic media and others follow our citation guidelines when re-posting articles from farmdoc daily. Guidelines are available here. The farmdoc daily website falls under University of Illinois copyright and intellectual property rights. For a detailed statement, please see the University of Illinois Copyright Information and Policies here.







